Предлагаемые ответы по математике для вступительного экзамена в 10-й класс в Ханое в 2025 году

Департамент образования и профессиональной подготовки Ханоя опубликовал примеры вопросов по 7 предметам для вступительного экзамена в 10-й класс в 2025 году. Эти 7 предметов включают литературу, математику, иностранные языки, естественные науки, историю и географию, обществознание и информационные технологии.

Наглядный пример экзамена по математике для поступления в 10-й класс в 2025 учебном году в Ханое (скриншот).

По математике знание экзамена состоит из 3 частей: числа и алгебра — 4,5 балла, геометрия и измерения — 4 балла, статистика и вероятность — 1,5 балла.

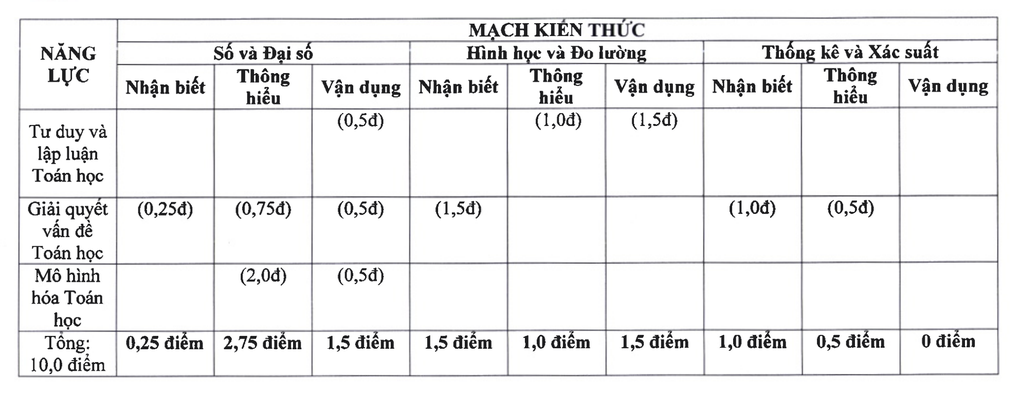
Тест на знание математики для вступительного экзамена в 10-й класс в Ханое в 2025 году (скриншот).

>> Подробные предлагаемые ответы на экзамен по математике для государственных 10-х классов в Ханое в 2025 году от преподавателей профессионального отдела tuyensinh247 см. ЗДЕСЬ

Обзор теста по математической иллюстрации

По словам преподавателя До Ван Бао, общая структура экзамена выглядит следующим образом:

Часть I: (1,5 балла) Включает 2 вопроса по статистике и вероятности.

- Статистика данных, диаграммы

- Вероятность

Часть II: (1,5 балла) Включает 3 вопроса по алгебраическим выражениям, аналогичные вопросу I на экзаменах прошлых лет.

- Вычислить значения выражений, проверить базовые навыки учащихся

- Упростить выражение

- Дополнительные вопросы для дифференциации студентов

Часть III: (2,5 балла) Включает 3 вопроса, связанных с системами уравнений и квадратными уравнениями.

- Вопрос 1,2: Решите реальные задачи, составив систему уравнений, составив уравнения

- Вопрос 3 Квадратное уравнение

Урок IV. Геометрия

- Пространственная геометрия

- Задачи об окружностях

Урок V. Сложные задачи на геометрический экстремум, связанные с практическими факторами.

Общая оценка: 10 баллов, равномерно распределенных между базовыми и углубленными разделами знаний, от алгебры, геометрии до практических приложений.

Комментарии по содержанию знаний

Раздел «Алгебра»: включает базовый контент, такой как вычисления с выражениями, квадратные уравнения и приложения. Новым моментом иллюстративного теста является то, что в нем много вопросов, которые затрагивают проблемы реальной жизни, помогая учащимся подходить к решению жизненных проблем через математику.

Раздел геометрии: Включает знакомый контент, такой как планиметрия, задачи, связанные с окружностями и вписанными четырехугольниками, пространственная геометрия, геометрические доказательства и геометрические приложения на практике. Экзамен требует от студентов хорошего пространственного мышления и умения применять геометрическую теорию к практическим задачам.

Раздел «Статистика и вероятность»: представляет собой новый материал по сравнению с экзаменами прошлого года, представленный в Уроке I, требующий от студентов анализа графиков и расчета вероятности, который предполагает практическое применение и часто встречается в новых программах учебников.

Комментарии по сложности

Базовый и средний уровень: вопросы по оценке выражений, решению квадратных уравнений и вычислению вероятности относятся к базовому и среднему уровню. Чтобы ответить на эти вопросы, студентам необходимо овладеть лишь базовыми знаниями.

Продвинутый уровень: вопросы по геометрическим доказательствам, практические задачи, связанные с пространственной геометрией, и задачи по расчету банковских процентов требуют от студентов хорошего логического мышления и умения применять знания на практике. Эти вопросы часто будут сложными для обычных учеников.

Образец экзамена в Ханое разработан таким образом, чтобы максимально точно соответствовать новой общеобразовательной программе и уделять особое внимание всесторонней проверке знаний и навыков учащихся, особенно их способности применять их на практике.

Экзамен сохраняет 60–70 % традиционной структуры, но в него внесены новшества в содержание и методы составления вопросов, что позволяет более комплексно оценивать учащихся.

Уровень сложности экзамена умеренный, с четкой дифференциацией для отбора хороших студентов.

В предыдущие годы на экзамене часто проводилось четкое различие между хорошими и средними учениками с помощью вопросов по чистой алгебре и геометрии. В пробный тест добавлен практический элемент, требующий от студентов не только наличия знаний, но и понимания того, как применять эти знания в конкретных ситуациях.

Структура иллюстративного экзамена в этом году была существенно обновлена ​​по сравнению с предыдущими годами: была проведена классификация содержания знаний на уроках, чередование типов вопросов и, в особенности, увеличение количества практических задач. Это отражает направление новой образовательной программы, которая больше фокусируется на проверке способности учащихся применять знания и синтезировать мышление.

Чтобы успешно сдать экзамен, ученикам 9-го класса необходимо:

Чтобы хорошо подготовиться к вступительному экзамену в 10-й класс, имеющему ту же структуру и содержание, что и типовой экзамен, ученикам 9-го класса необходимо выполнить следующие шаги:

1. Освойте основы

Алгебра: Необходимо освоить базовые знания по программе 9-го класса, в том числе:

Уравнения первой и второй степени, решения и свойства.

Формулы, относящиеся к плоской и стереометрии, особенно теоремы, относящиеся к треугольникам, окружностям и основным геометрическим фигурам.

Решайте проблемы, составляя уравнения

Геометрия: Знания, теоремы об окружностях, вписанных четырехугольниках и их свойствах, доказательство подобия треугольников и применение свойств подобия треугольников,...

Статистика и вероятность: вам необходимо быть знакомым с основными статистическими концепциями, такими как графики частот, таблицы частот и простые вычисления вероятностей, поскольку эти области могут встретиться на экзамене.

2. Практикуйтесь в решении реальных математических задач

Прикладная математика: студентам необходимо практиковаться в решении задач, связанных с реальной жизнью, решении задач путем составления уравнений, систем уравнений, производственных и управленческих задач или задач, связанных с пространственной геометрией.

Применяйте знания на практике: решайте практические задачи, связанные с измерением и вычислением объема и площади. Это помогает учащимся лучше понять, как математика применяется в жизни.

3. Практикуйте логическое мышление и аналитические навыки.

Математическое доказательство: расширение практики решения задач геометрического и алгебраического доказательства. В частности, задачи, требующие демонстрации взаимосвязей между элементами плоской или пространственной геометрии, имеют важное значение для развития логического мышления.

Анализируйте и решайте проблемы: практикуйтесь в анализе проблемы, четко понимая требования каждого вопроса, прежде чем приступать к ее решению. Это помогает избежать путаницы и повышает точность во время теста.

Источник: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm