수학은 8, 9점이 많을 것이다

빈스쿨과 온라인 학습 사이트 Tuyensinh247의 교사인 도 반 바오(Do Van Bao) 교사에 따르면, 올해 하노이의 10학년 입학 시험을 위한 수학 시험은 작년과 비교해 구조가 크게 바뀌지 않아 다소 "쉬워졌습니다". 이 시험은 학생들의 수준을 차별화하지만 여전히 쉽고 8점과 9점이 많이 나옵니다.

6월 11일 오전 수학 시험을 마치고 사랑하는 사람들의 품에 안긴 수험생들.

전반적으로 이 시험은 학생 평가 요건을 충족하며 차별화 요소가 있습니다. 기본 지식과 기술을 시험하는 내용이 높아 학생들에게 너무 어렵지 않습니다. 학생들에게는 기본 수학 문제를 잘 풀고, 복습할 시간만 있으면 되며, 시험을 주의 깊게 치르면 시험의 75~80%를 신속히 완료할 수 있습니다. 몇 가지 차별화된 질문이 있기는 하지만 너무 어렵지 않으므로 지원자는 여전히 해결책을 생각해낼 수 있습니다.

평균적인 학생은 처음 세 번의 시험에서 좋은 성적을 거둘 수 있습니다.

1과, 표현식을 간소화하고 표현식 값 계산은 이미 알려진 결과인 상당히 간단한 표현식을 간소화하고 값을 계산하는 것에 대한 기본 지식의 일부로, 학생들이 쉽게 점수를 받을 수 있도록 꼼꼼한 학습을 ​​할 수 있는 여건을 마련해줍니다. 학생들은 단지 주의 깊게 연습하고 첫 번째 아이디어에서 그것을 완벽하게 제시하기만 하면 됩니다.

두 번째로, 이 문제는 이미 결과가 알려진 식을 단순화하도록 요구하므로 학생들이 실수를 하기 어렵습니다. 세 번째 아이디어는 다른 유형의 방정식보다 쉬운 2차 방정식을 푸는 기술을 테스트하여 학생들이 이 시험에서 쉽게 만점을 받을 수 있도록 하는 것입니다.

2과에서는 방정식 체계를 설정하여 문제를 푸는 실제적인 문제입니다. 문제 1은 업무 생산성과 관련된 방정식이나 방정식 시스템을 만들어서 문제를 해결하는 유형입니다. 학생들은 방정식계 또는 방정식계를 설정하는 문제를 쉽게 분석하고 방정식/방정식계를 풀어 이 문제에서 최고 점수를 달성할 수 있습니다. 일부 학교의 질적 평가 및 모의고사에서는 문제 유형 1이 자주 출제되어 학생들이 연습하기에 좋은 환경을 제공합니다.

2번 문제는 구체 지식과 관련된 간단한 실용 문제입니다. 학생들은 구의 부피를 계산하는 공식만 기억하고 주의 깊게 계산하여 점수를 얻으면 됩니다.

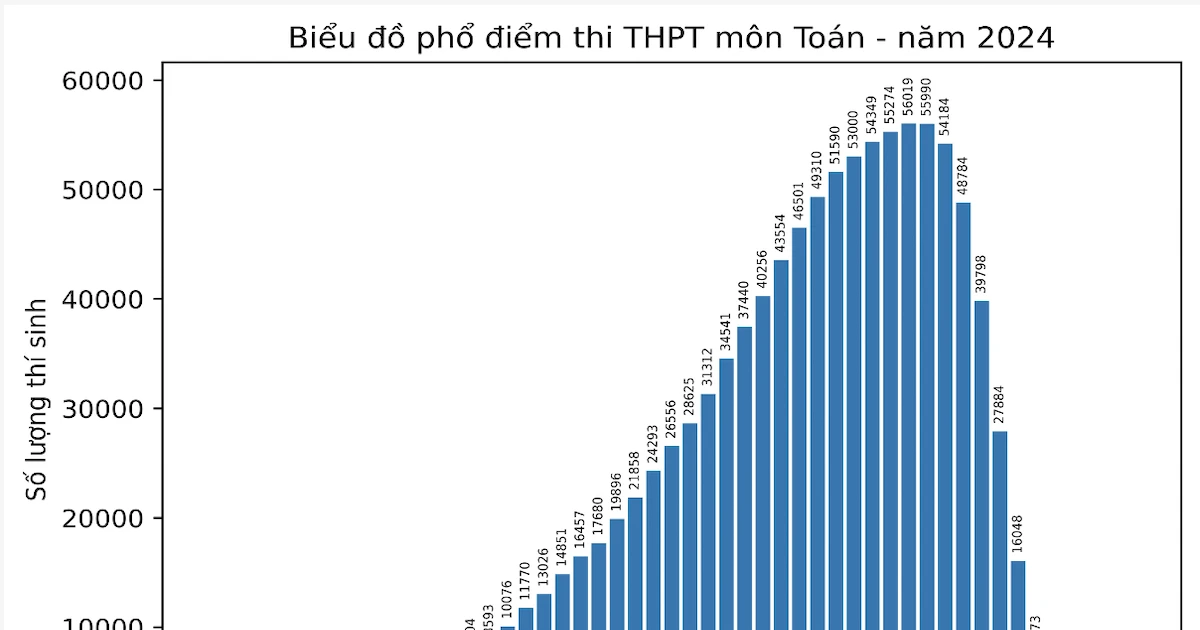
하노이 교육훈련부가 주관하는 2023년 10학년 입학 시험을 위한 수학 시험

3과는 방정식 시스템과 함수 그래프에 관한 내용입니다. 이것은 점수를 매기기 매우 간단하고 쉬운 연습입니다. 문제 1에서 학생들은 종종 보조 변수 방법을 사용하여 문제를 풉니다. 또한 학생들은 프레젠테이션에 주의를 기울여야 하고, 미지수의 조건을 고려하고, 최대 점수를 얻기 위해 최종 해결책을 결론내야 합니다. 평균 이상의 학생이라면 이 문제에서 좋은 성적을 거둘 수 있습니다.

3과의 2번 질문은 포물선과 익숙한 직선의 교점에 대한 지식과 관련이 있습니다. 평균 이상의 학생은 이 문제의 a 부분에서 좋은 점수를 받을 수 있고, 우수한 학생은 b 부분에서 좋은 점수를 받을 수 있는데, 그 이유는 표현식이 두 해 사이의 대칭성 조건을 만족하고, 비에트 정리를 적용하기 위해 두 해의 합과 곱으로 변환될 수 있기 때문입니다. 그러나 최대 점수를 얻으려면 신중한 프레젠테이션과 철저한 주장에 주의를 기울이는 것이 필요합니다.

학생들의 차별화는 수업 4와 5에 집중되어 있습니다.

4과에서는 기하학 연습이 나오는데, 꽤 괜찮은 기하학 연습이고, 마지막 아이디어에서 학생들을 잘 분류해 놓았습니다. 기하학 문제는 익숙한 원이나 반원에서 시작하지 않지만, 대신 문제 1과 2를 풀 때 제안하는 많은 요소가 있습니다. 학생들은 문제의 요구 사항을 주의 깊게 읽고, 1번 지점을 풀 수 있는 모양을 주의 깊게 그립니다. 왜냐하면 이 지점은 복습 과정에서 꽤 익숙한 기본 지식이고 학교의 설문 조사와 모의 시험에서 꽤 자주 나오기 때문입니다.

아이디어 2는 학생들에게 더 많은 사고를 요구합니다. 학생들은 평행 관계와 내접 사각형을 기반으로 각도가 동일하다는 것을 증명하기 위해 주장해야 합니다.

아이디어 3은 학생 분류가 비교적 명확합니다. 학생들은 삼각형의 중선을 도출하기 위해 중간점 인수를 적용하는 데 주의를 기울여야 하며, 거기에서 동일한 대응각을 도출하여 순환 사각형을 도출하고, 유사한 삼각형을 증명하여 동일한 곱을 도출해야 합니다. 평행성 증명이라는 하위 아이디어에서, 학생들은 이 아이디어를 완성하기 위해 같은 각의 인수를 기반으로 한 내접 사각형을 증명해야 합니다. 이 부분에서 학생들은 각은 같은 각의 합과 같다는 속성에 기초한 중간 수준의 증명에 의지할 수 있습니다.

5과에서는 극단값에 대한 꽤 괜찮은 문제지만 너무 어렵지는 않습니다. 이런 유형의 수학은 우수한 학생들에게 꽤 익숙합니다. 표현식과 조건은 a와 b 사이에서 대칭적이며, 문제는 또한 학생들이 증명에 집중할 수 있도록 왼쪽의 최대값을 제공합니다. 하지만 이는 합의 가장 큰 값을 찾는 형태로, 코사인 부등식을 직접 적용하는 사고방식에 비해 약간 "뒤떨어진" 감이 있습니다. 학생들은 다양한 방법으로 접근할 수 있습니다.

바오 선생님은 "올해 수학 시험은 학생들을 차별화하지만 여전히 쉽습니다. 올해는 8점과 9점이 많을 것이지만 대부분은 6.5-8점일 것입니다. 시간을 잘 관리하고, 신중하게 계산하고, 충분히 발표하면 우수한 학생은 8점 이상을 받을 수 있습니다. 시험이 "더 쉬운" 까닭에 시험을 채점하는 교사는 발표 오류에 대한 점수를 감점하는 데 더 많은 주의를 기울이기 때문에 점수가 약간 낮을 것입니다."라고 말했습니다.

소스 링크: https://thanhnien.vn/thi-vao-lop-10-o-ha-noi-mon-toan-se-co-nhieu-diem-8-9-185230611143505637.htm