Lernen die Schüler „Mathematik ohne nachzudenken“?

GIBT ES EINE ART „NICHT-DENKENDER“ MATHEMATIK?

Dr. Nguyen Phi Le (Fakultät für Informations- und Kommunikationstechnologie, Hanoi University of Science and Technology) war einst ein guter Mathematikstudent und gewann im Jahr 2000 eine Silbermedaille beim internationalen IMO-Mathematikwettbewerb, ohne allzu viele zusätzliche Kurse belegen zu müssen. Als sein Kind noch in der Grundschule war, war Dr. Le daher nicht der Meinung, dass sein Kind zusätzlichen Mathematikunterricht im Allgemeinen und „Denkmathematik“ im Besonderen belegen müsse, obwohl zu dieser Zeit auf dem Nachhilfemarkt viele Zentren auftauchten, die mit dem Unterrichten von „Denkmathematik“ warben. Als mein Kind jedoch in der 5. Klasse war und später die Abschlussprüfung der 10. Klasse ablegte, war Dr. Le gezwungen, meinem Kind zusätzlichen Mathematikunterricht zu gewähren, da es nur dann die Aufnahmeprüfung für Spezialschulen und Auswahlklassen bestehen konnte.

Viele Eltern lassen ihre Kinder schon in jungen Jahren mathematisches Denken lernen, in der Hoffnung, dass ihre Kinder in Mathematik gute Leistungen erbringen.

„Beispielsweise diskutierten Lehrer und Schüler kürzlich nach der Aufnahmeprüfung für die 10. Klasse im Fach Mathematik an der High School for Natural Sciences der University of Natural Sciences der Vietnam National University in Hanoi viel über eine Geometriefrage. Ein guter Geometrielehrer sagte, er habe diese Frage drei bis vier Stunden lang bearbeitet. Ein Schüler der 9. Klasse musste sie jedoch in kurzer Zeit lösen. Wenn ein Schüler nicht an Übungsprüfungen teilgenommen und noch nie ähnliche Fragen bearbeitet hatte, konnte er diese Prüfung definitiv nicht bewältigen. Selbst ein Schüler mit sehr guten Denkfähigkeiten konnte nicht

Machen Sie in kurzer Zeit eine sehr schwierige Übung mit einer ungewöhnlichen Form. „Um eine solche Aufgabe zu erledigen, braucht man viel Zeit“, teilte Dr. Le mit.

Dr. Le sagte außerdem, dass sie ihrem Kind, wenn es zu viele zusätzliche Unterrichtsstunden nahm, geraten habe, mehr Zeit mit dem selbstständigen Lernen zu verbringen, weil das Gehirn des Lernenden nur dann Zeit habe, das Wissen aufzunehmen, was dem Lernenden helfe, selbstständig zu sein und später bei der Lösung von Problemen die Fähigkeit zur Unabhängigkeit zu haben. Ihr Kind war jedoch nicht beruhigt, weil es befürchtete, dass es bei einem Rennen, bei dem die Schüler im Vorteil waren, die im Prüfungsvorbereitungsunterricht hart arbeiteten, nicht mit seinen Freunden mithalten könnte.

Laut Professor Le Anh Vinh, Direktor des Vietnam Institute of Educational Sciences, reagieren viele Mathematiker allergisch, wenn jemand „denkende Mathematik“ sagt. Denn zu sagen, dass sich das herausstellt, ist „Mathematik ohne Denken“? Die Realität ist jedoch, dass es in den aktuellen Lehrmethoden viele Arten des Mathematikunterrichts gibt, bei denen nicht das Denken, sondern nur das Rechnen gelehrt wird. Im Unterricht bringen Lehrer ihren Schülern oft vor allem das Bearbeiten von Übungen nach Modellen bei (oft auch „Formenrechen“ genannt). Mit dieser Lehrmethode können Schüler, die eine bestimmte Art von Matheaufgabe schon einmal gelöst haben, diese normalerweise sehr schnell lösen, wenn sie erneut darauf stoßen, ohne überhaupt darüber nachdenken zu müssen.

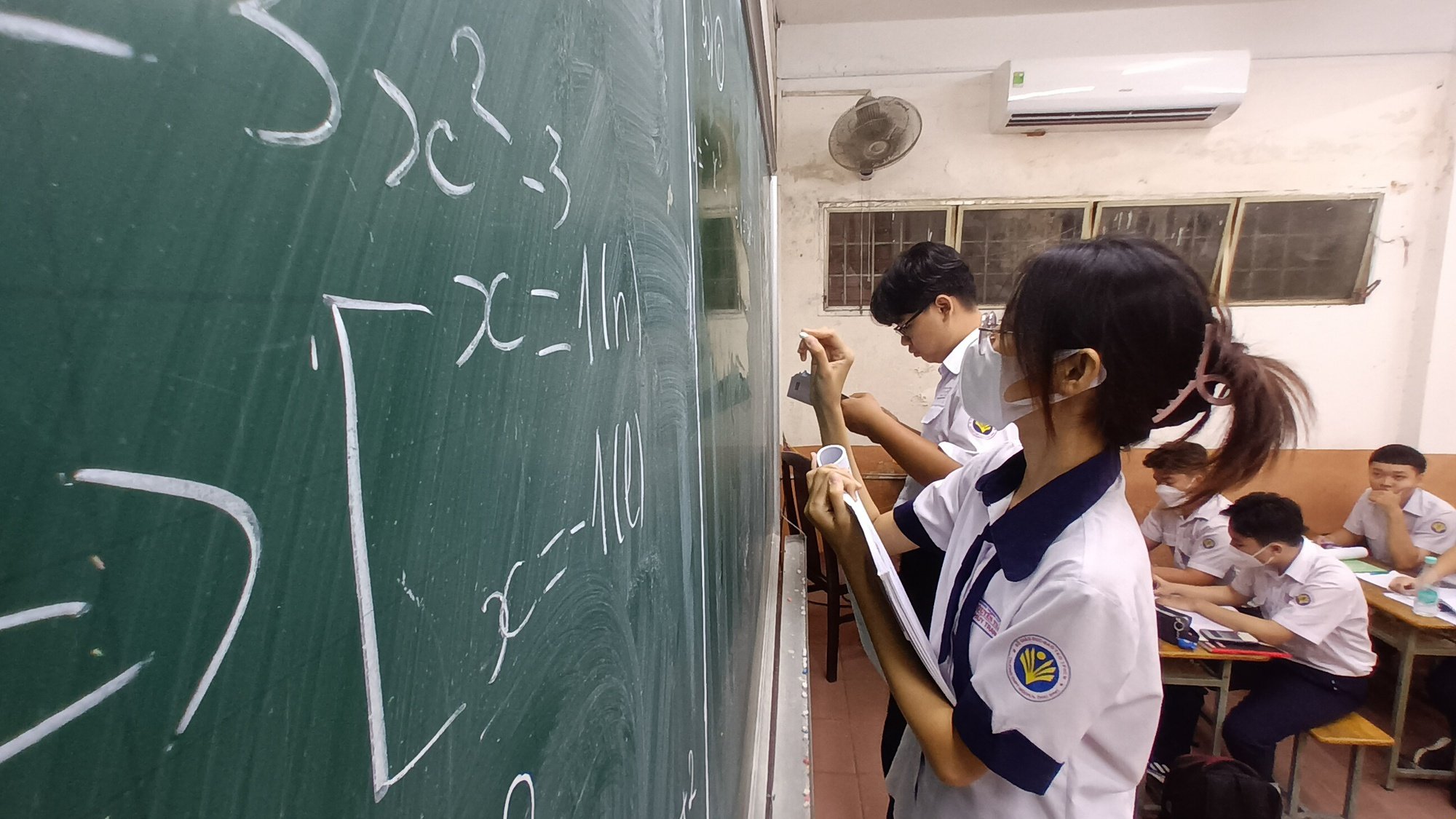
Im Mittelpunkt des neuen allgemeinbildenden Programms steht die Mathematik in Verbindung mit der Praxis, mit der Anwendung und mit der Lösung der Frage, wozu Mathematik dient, und nicht nur mit dem bloßen Ausführen von Übungen.

WENN DAS LERNEN VON MATHEMATIK NICHT MEHR DIE NATUR DES LERNENS VON MATHEMATIK IST

Laut Dr. Vu Thi Ngoc Ha vom Institut für Angewandte Mathematik und Informatik der Hanoi University of Science and Technology fördert jedes naturwissenschaftliche Fach die Entwicklung und Vervollkommnung des Denkens jedes Kindes. Man spricht hier von einer „Vielfalt der grundlegenden Felder“, und es geht nicht nur darum, Mathematik zu lernen, um das Denken zu entwickeln.

Allerdings haben die Probleme in der Mathematik immer einen Bezug zur Realität. Um zu bestehen, muss das Kind die Schritte zur Konstruktion eines Problems auf Grundlage der Analyse der Gesetze natürlicher Phänomene durchlaufen und dann logisches Denken, kreatives Denken usw. einsetzen, um das Problem zu lösen. Im oben beschriebenen Prozess kann manchmal die Anregung der Vorstellungskraft und des kritischen Denkens zur Lösung des gegebenen Problems beitragen.

„Mathematik selbst scheint das Fach zu sein, das das Denken am besten anregt. Daher ist die Entstehung von Zentren für „mathematisches Denken“ in der heutigen Situation verständlich, in der wir uns der Aufgabe stellen müssen, in kürzester Zeit ein bestimmtes Wissensmodul jedes Fachs zu beherrschen – nicht nur Mathematik –, um Prüfungen zu bestehen. Dies führt zu einer Art des Mathematiklernens, die nicht mehr dem Wesen des „Mathematiklernens“ entspricht“, kommentierte Dr. Ngoc Ha.

Professor Le Anh Vinh sagte, dass er anfangs auch gegen das Wort „mathematisches Denken“ allergisch reagierte. Später, nach Recherchen, fand ich heraus, dass es immer noch eine ziemlich verbreitete Methode gibt, Mathematik ohne Nachdenken zu unterrichten. Professor Vinh kommentierte: „Wenn wir sagen, dass wir hier Mathematik unterrichten und nicht Mathematik ohne Nachdenken, klingt das zu schwerfällig. Wenn sich also jemand oder irgendwo als Lehrer für Denkmathematik vorstellt, bedeutet das, dass er Mathematik im wahrsten Sinne des Wortes unterrichten möchte. ‚Denkmathematik‘ rührt daher, dass die Leute Mathematik so unterrichten möchten, dass die Schüler nachdenken und die Mathematik im Leben anwenden können, und nicht Mathematik in einer Form, damit die Schüler wirklich gute Prüfungsergebnisse erzielen. Auch Eltern sollten darüber nachdenken, denn wenn sie sich so vorstellen, bedeutet das, dass sie ihren Schülern nicht beibringen, Mathematik zu lernen, um gute Prüfungsergebnisse zu erzielen, sondern ihnen das Nachdenken beizubringen.“

C Notwendigkeit einer Innovation des Prüfungssystems

Dr. Ngoc Ha ist davon überzeugt, dass die Schüler „langsam lernen“ müssen, damit das Mathematiklernen wieder zu seiner wahren Natur zurückfindet, denn „langsames Lernen“ ist der beste Weg, die Entwicklung des Denkens jedes Kindes zu fördern.

Wenn die Schüler mit einem Problem konfrontiert werden, müssen sie Zeit (sehr viel Zeit) haben, um Naturphänomene zu identifizieren, von dort aus nach Mengen und Gesetzen zu suchen, um mithilfe von Ausdrücken Beziehungen zwischen Mengen herzustellen, und dann nach Werkzeugen und Methoden zur Lösung des Problems zu suchen. Daher ist es sehr schwierig, ein Programm mit dem Namen „Kopfrechnen“ zu erstellen. Doch das Unterrichten ist noch schwieriger, denn neben der „langsamen, sehr langsamen“ Führung muss der Lehrer auch über ein hohes Maß an Allgemeinwissen verfügen. Der Unterricht muss flexibel und den Fähigkeiten jedes einzelnen Schülers angemessen sein. Dies ist sehr schwierig, wenn die schulischen Leistungen, Noten und Erwartungen der Eltern einen hohen Druck auf die Zeit des Kindes ausüben ...

Bringen Sie den SCHÜLERN das Denken bei, nicht das Rechnen.

Professor Le Anh Vinh scherzt oft mit Mathematiklehrern: Schülern 10 Minuten lang das Denken beizubringen, ist schwieriger, als ihnen beizubringen, eine Stunde lang zu sitzen und zu rechnen. Wenn es in der Schule nur darum geht, ein Arbeitsblatt zu bekommen und sich dann hinzusetzen und auszurechnen, wie man es schnell und gut lösen kann, dann bleibt nach dem Unterricht nichts im Gedächtnis des Schülers hängen. Wenn Schüler auf neue Situationen stoßen, können sie nicht nachdenken oder das Gelernte nicht anwenden, um Probleme zu lösen. Allerdings handelt es sich hierbei um ein systematisches Problem, das aus der Geschichte der Prüfungen, Tests und Übungen hervorgeht und dazu führt, dass beim Unterrichten alle Teile übersprungen werden, die das Denken entwickeln, und man sich nur darauf konzentriert, den Schülern das Rechnen und das Lösen von Übungen beizubringen.

Insbesondere erfordert der Mathematikunterricht als Denkunterricht die Synchronisierung eines gesamten Systems: Programm, Lehrbücher, Zeit für jede Stunde, jede Minute, jedes Fach, Prüfungssystem, Sozialpsychologie …

Kandidaten der 9. Klasse in Ho-Chi-Minh-Stadt im Mathematik-Prüfungsraum der letzten Aufnahmeprüfung für die 10. Klasse. Diese Mathematikprüfung enthält viele praktische Aufgaben.

Laut Professor Vinh konzentriert sich das neue allgemeine Bildungsprogramm auf Mathematik in Verbindung mit der Praxis, mit der Anwendung und mit der Lösung der Frage, wozu Mathematik dient, und nicht nur auf das bloße Ausführen von Übungen.

Dr. Phi Le sagte, dass sie Studenten dabei unterstützt, zusätzliche Kurse in Fächern zu belegen, die sie interessieren und zu denen sie befähigt sind, aber auf eine Art und Weise, die ihre Kreativität und Denkfähigkeit fördert. Und die derzeitige Art des zusätzlichen Lernens in Form von Prüfungsvorbereitungen ist für die Studierenden nicht sehr nützlich. Das Problem besteht darin, dass die aktuelle Fragenstellung Studierende, die die Prüfungsfragen nie gelernt haben, zu „Verlierern“ macht. Im aktuellen Prüfungsumfeld herrscht ein ungleicher Wettbewerb zwischen Studierenden, die „denken“ lernen, und Studierenden, die für die Prüfung üben. Denken kostet viel Zeit und man geht das Risiko ein, viele Fragen nicht zu kennen. Dies ist die „Motivation“, die Studierende dazu zwingt, zusätzliche Kurse zu belegen.

Wie sollten also Prüfungen gestaltet werden, um das Denken der Schüler zu fördern? „Die Prüfungsfragen sollten nicht schwierig sein, mit den Inhalten der allgemeinen Schulen übereinstimmen und auch Schüler mit guten Denkfähigkeiten erkennen“, sagte Dr. Phi Le.

Quellenlink: https://thanhnien.vn/phai-chang-hoc-sinh-dang-hoc-toan-khong-tu-duy-185230609045433219.htm