អ្នកវិទ្យាសាស្ត្រស្វែងរកដំណោះស្រាយចំពោះបញ្ហាធរណីមាត្របុរាណដែលមានរយៈពេលជាងមួយសតវត្ស

រូបភាពសម្រាប់បញ្ហាធរណីមាត្រ។

យោងតាមកាសែត South China Morning Post គណិតវិទូ Hong Wang ដែលបច្ចុប្បន្នជាសាស្ត្រាចារ្យរងនៅវិទ្យាស្ថាន Courant សម្រាប់វិទ្យាសាស្ត្រគណិតវិទ្យានៃសាកលវិទ្យាល័យញូវយ៉ក (សហរដ្ឋអាមេរិក) និងសហការីរបស់គាត់ Joshua Zahl (University of British Columbia, Canada) ទើបតែបានដោះស្រាយបញ្ហាធរណីមាត្រដ៏លំបាកបំផុតមួយនៃសតវត្សទី 20-21: Consultational the 20th-21st. លំហ។

Hong Wang កើតនៅទីក្រុង Guilin (ប្រទេសចិន) បានសិក្សានៅសាកលវិទ្យាល័យ Peking មុនពេលបង្រៀន និងស្រាវជ្រាវនៅសហរដ្ឋអាមេរិក។

បញ្ហានេះកើតឡើងនៅឆ្នាំ 1917 នៅពេលដែលគណិតវិទូជនជាតិជប៉ុន Soichi Kakeya បានសួរសំណួរថា "តើតំបន់តូចបំផុតដែលត្រូវការបង្វិលម្ជុល 180 ដឺក្រេ? ចន្លោះតូចបំផុតនោះត្រូវបានគេហៅថា "Kakeya set" ។

នៅក្នុងលំហពីរវិមាត្រ ការបង្វិលម្ជុលដើម្បីបង្កើតជារង្វង់គឺងាយស្រួលមើលឃើញ ប៉ុន្តែប្រសិនបើការបង្វិលមានភាពបត់បែនជាងមុន ដូចជាការគ្រវីម្ជុលនៅពេលបង្វិល តំបន់ដែលម្ជុលអាចមានទំហំតូចជាង។

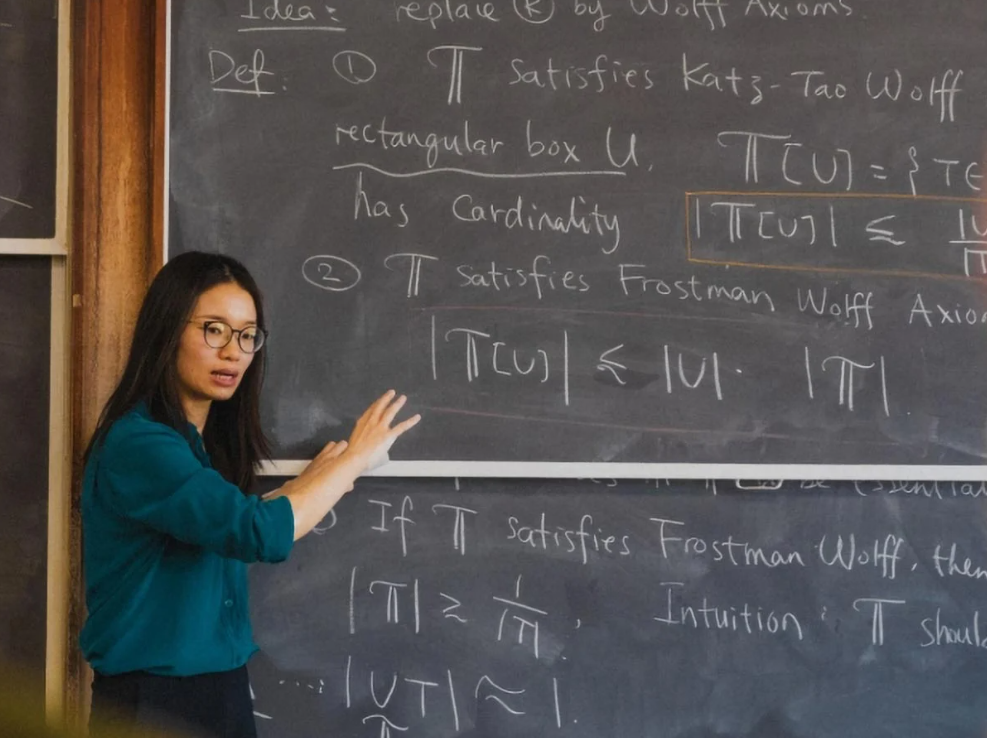
អ្នកវិទ្យាសាស្ត្រស្វែងរកដំណោះស្រាយចំពោះបញ្ហាធរណីមាត្រដែលមានរយៈពេលជាងមួយសតវត្ស។

នៅពេលដែលបញ្ហាត្រូវបាននាំមកជាបីវិមាត្រ នោះបញ្ហាកាន់តែស្មុគស្មាញ។ ការស្មានរបស់ Kakeya និយាយថា ប្រសិនបើអ្នកចង់បង្វិលម្ជុលនៅគ្រប់ទិសទី ចន្លោះដែលត្រូវការត្រូវតែធំល្មមគ្រប់ទំហំទាំងបី - វាមិនអាចច្របាច់ចូលទៅក្នុងកន្លែងដែលតូចពេក ឬស្តើងពេកនោះទេ។

នៅក្នុងក្រដាសមួយដែលបានចេញផ្សាយនាពេលថ្មីៗនេះនៅលើវេទិកា arXiv លោក Wang និង Zahl បង្ហាញថា ក្នុងចន្លោះបីវិមាត្រ តំបន់សម្រាប់ការបង្វិលម្ជុលមិនចាំបាច់មានរូបរាងច្បាស់លាស់ទេ ប៉ុន្តែត្រូវតែមានទំហំធំល្មមក្នុងគ្រប់ទំហំទាំងបី។ អរគុណចំពោះបញ្ហានេះ ពួកគេបានដោះស្រាយបញ្ហានេះ - នេះត្រូវបានចាត់ទុកថាជារបកគំហើញដ៏សំខាន់មួយនៅក្នុងគណិតវិទ្យាសព្វថ្ងៃនេះ។

សាស្ត្រាចារ្យ Terence Tao ដែលជាគណិតវិទូឈានមុខគេរបស់ពិភពលោកបានហៅវាថា "វឌ្ឍនភាពដ៏អស្ចារ្យ" ។ អ្នកជំនាញក៏បាននិយាយផងដែរថា ការងារនេះមិនត្រឹមតែពង្រីកការយល់ដឹងអំពីធរណីមាត្រប៉ុណ្ណោះទេ ថែមទាំងអាចប៉ះពាល់ដល់វិស័យជាច្រើនដូចជា ដំណើរការរូបភាព ទំនាក់ទំនងឥតខ្សែ វិទ្យាសាស្ត្រកុំព្យូទ័រ និងគ្រីបគ្រីប ដែលការយល់ដឹងអំពីចលនា និងអន្តរកម្មក្នុងលំហគឺមានសារៈសំខាន់ខ្លាំងណាស់។

សាស្ត្រាចារ្យគណិតវិទ្យា Nets Katz ដែលបង្រៀននៅសាកលវិទ្យាល័យ Rice (សហរដ្ឋអាមេរិក) បាននិយាយថា "មិនមែននិយាយបំផ្លើសទេ ប៉ុន្តែនេះគឺជាដំណោះស្រាយដ៏កម្រមួយ ដែលយើងរង់ចាំរាប់រយឆ្នាំដើម្បីលេចចេញជារូបរាង"។

យោងតាមសាស្ត្រាចារ្យ Guth Larry សាស្ត្រាចារ្យនៅវិទ្យាស្ថានបច្ចេកវិទ្យា Massachusetts (សហរដ្ឋអាមេរិក) សម្មតិកម្ម Kakeya គឺជាមូលដ្ឋានគ្រឹះនៃ "ប៉ម" នៃសម្មតិកម្មធំជាងនៅក្នុងវិស័យធរណីមាត្រ។ ការ​ដោះស្រាយ​សម្មតិកម្ម​នេះ​នឹង​ផ្តល់​ឱ្យ​កម្រិត​ខ្ពស់​នៃ​ប៉ម​ចំណេះ​ដឹង​នូវ​ឱកាស​ត្រូវ​បាន​គេ​ខិត​ជិត​និង​ដណ្តើម​យក​បាន។

"ខ្ញុំធ្លាប់គិតថានេះជាបញ្ហាធរណីមាត្រសាមញ្ញធម្មតា ប៉ុន្តែតាមពិត បញ្ហានេះពិបាកពេក។ បញ្ហានេះត្រូវបានបន្តដោយឈ្មោះធំៗជាច្រើនក្នុងគណិតវិទ្យា ប៉ុន្តែភាគច្រើនពួកគេសម្រេចបានតែលទ្ធផលតូចតាច មិនមែនជាប្រព័ន្ធ និងមិនអាចចាត់ទុកថាជាដំណោះស្រាយពេញលេញនោះទេ"។

Phuong Anh (ប្រភព៖ Science Daily, SCMP)

ប្រភព៖ https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-geometry-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html