Le lycée pour les surdoués en sciences naturelles annonce les résultats de référence de la 10e année

Le soir du 12 juin, le lycée des sciences naturelles a annoncé les résultats d'admission pour la 10e année, dans laquelle la classe de mathématiques a obtenu le score le plus élevé avec 19,5 points.

Điểm chuẩn lớp 10 chuyên Khoa học Tự nhiên

Le lycée pour les surdoués en sciences naturelles a annoncé les scores de référence pour la 10e année spécialisée. (Source : VNU)

Vient ensuite l'IT avec 19,25 points. Les cours spécialisés en physique, chimie et biologie coûtent respectivement 16,25 $ ; 15 et 15 points. Le score de référence de 15 est également le plus bas des 7 dernières années de l'École secondaire des sciences naturelles.

Les notes d'admission spécifiques pour la 10e année du lycée des sciences naturelles sont les suivantes :

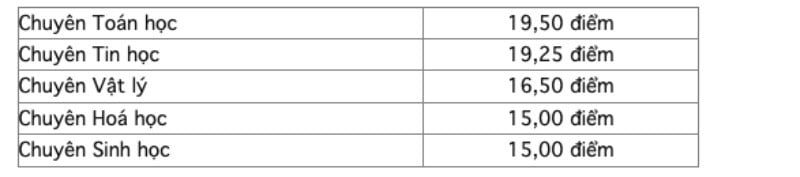Score standard pour la 10e année spécialisée en sciences naturelles.

Les 4 et 5 juin, près de 3 000 candidats ont passé l'examen d'entrée en 10e année au Lycée des Sciences Naturelles. Les candidats doivent passer des examens en mathématiques, en littérature (1er tour) et dans des matières spécialisées (2e tour). Le score d'admission est la somme du score en mathématiques du premier tour et de la matière spécialisée multipliée par le coefficient 2, maximum 30 points. Le score littéraire n'est qu'une condition, il n'est pas pris en compte dans le score d'admission. Les candidats sont admissibles à l'admission en passant les trois examens, sans aucune matière inférieure à 4. L'école n'ajoute pas de points de priorité.

En plus de 5 classes spécialisées, chaque classe accueille 90 élèves, le Lycée des Surdoués en Sciences Naturelles dispose d'une classe de haute qualité. L'école sélectionne les candidats qui ont postulé à ce programme et qui ont obtenu un score de 4 ou plus au premier tour de littérature et de mathématiques. Ces étudiants passeront un test de QI supplémentaire de 60 minutes et un entretien en face à face.

Le score d'admission pour la classe de haute qualité est le score total de Littérature, QI et entretien (coefficient 1) plus le score de Mathématiques tour 1 (coefficient 2), maximum 50 points.

Source