Réponses mathématiques suggérées pour l'examen d'entrée en 10e année à Hanoi en 2025

Le ministère de l'Éducation et de la Formation de Hanoi a annoncé des exemples de questions pour 7 matières pour l'examen d'entrée en 10e année en 2025. Ces 7 matières comprennent la littérature, les mathématiques, les langues étrangères, les sciences naturelles, l’histoire et la géographie, l’éducation civique et l’informatique.

Examen de mathématiques illustratif pour l'examen d'entrée en 10e année pour l'année scolaire 2025 à Hanoi (capture d'écran).

Pour les mathématiques, les connaissances de l'examen se composent de 3 parties : Les nombres et l'algèbre comptent pour 4,5 points, la géométrie et la mesure comptent pour 4 points, les statistiques et les probabilités comptent pour 1,5 point.

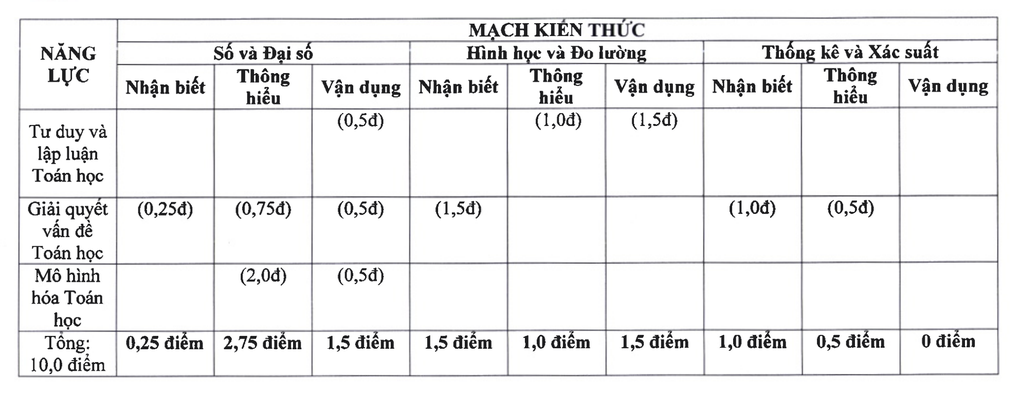
Circuit de connaissances mathématiques pour l'examen d'entrée en 10e année à Hanoi en 2025 (capture d'écran).

>> Voir les réponses détaillées suggérées pour l'examen de mathématiques pour la 10e année publique à Hanoi en 2025 par les enseignants du département professionnel de tuyensinh247 ICI

Révision du test d'illustration mathématique

Selon le professeur Do Van Bao, la structure générale de l'examen est organisée comme suit :

Partie I : (1,5 point) Comprend 2 questions sur les statistiques et les probabilités.

- Statistiques de données, graphiques

- Probabilité

Partie II : (1,5 point) Comprend 3 questions sur les expressions algébriques, similaires à la question I des examens des années précédentes.

- Calculer les valeurs des expressions, tester les compétences de base des élèves

- Simplifier l'expression

- Des questions supplémentaires pour différencier les élèves

Partie III : (2,5 points) Comprend 3 questions liées aux systèmes d’équations et aux équations quadratiques.

- Question 1,2 : Résoudre des problèmes réels en établissant un système d'équations, en établissant des équations

- Question 3 Équation quadratique

Leçon IV. Géométrie

- Géométrie spatiale

- Problèmes sur les cercles

Leçon V. Problèmes avancés sur les extrema géométriques liés à des facteurs pratiques.

Score total : 10 points, répartis uniformément entre les sections de connaissances de base et avancées, de l'algèbre, de la géométrie aux applications pratiques.

Commentaires sur le contenu des connaissances

Section Algèbre : Comprend du contenu de base tel que des calculs avec des expressions, des équations quadratiques et des applications. La nouveauté du test d'illustration est qu'il comporte de nombreuses questions qui exploitent des problèmes de la vie réelle, aidant les élèves à aborder les problèmes de la vie grâce aux mathématiques.

Section Géométrie : Comprend du contenu familier tel que la géométrie plane, les problèmes liés aux cercles et aux quadrilatères inscrits, la géométrie spatiale, les preuves géométriques et les applications géométriques dans la pratique. L'examen exige que les étudiants aient une bonne réflexion spatiale et la capacité d'appliquer la théorie géométrique à des problèmes pratiques.

Section Statistiques et probabilités : il s'agit d'un nouveau contenu par rapport aux examens de l'année précédente, apparaissant dans la leçon I, demandant aux étudiants d'analyser des graphiques et de calculer des probabilités, qui se contente d'applications pratiques et apparaît fréquemment dans les nouveaux programmes de manuels.

Commentaires sur la difficulté

Niveau de base et intermédiaire : les questions sur l’évaluation des expressions, la résolution d’équations quadratiques et le calcul des probabilités sont toutes de niveau de base et intermédiaire. Les étudiants n'ont besoin que de maîtriser les connaissances de base pour pouvoir répondre à ces questions.

Niveau avancé : Les questions sur les preuves géométriques, les problèmes pratiques liés à la géométrie spatiale et les problèmes de calcul des intérêts bancaires exigent que les étudiants aient une bonne pensée logique et la capacité d'appliquer leurs connaissances dans la pratique. Ces questions seront souvent difficiles pour les étudiants moyens.

L'examen type de Hanoi est conçu pour suivre de près le nouveau programme d'enseignement général, en mettant l'accent sur le test complet des connaissances et des compétences des étudiants, en particulier leur capacité à les appliquer dans la pratique.

L'examen conserve 60 à 70 % de la structure traditionnelle, mais a été innové dans le contenu et la rédaction des questions, contribuant ainsi à évaluer les étudiants de manière plus complète.

La difficulté de l’examen est modérée, avec une différenciation claire pour sélectionner les bons étudiants.

Au cours des années précédentes, l'examen faisait souvent une distinction claire entre les bons et les moyens élèves au moyen de questions d'algèbre et de géométrie pures. Le test simulé a ajouté un élément pratique, exigeant des étudiants non seulement d'avoir des connaissances, mais également de comprendre comment appliquer ces connaissances à des situations spécifiques.

La structure de l'examen illustratif de cette année a été considérablement innovée par rapport aux années précédentes, avec une classification du contenu des connaissances dans les leçons, un entrelacement des types de questions et surtout une augmentation des problèmes pratiques. Cela reflète l’orientation du nouveau programme d’enseignement, qui met davantage l’accent sur la capacité des étudiants à appliquer leurs connaissances et à synthétiser leur pensée.

Pour réussir à l'examen, les élèves de 9e année ont besoin :

Pour bien se préparer à l'examen d'entrée en 10e année avec la même structure et le même contenu que l'examen type, les élèves de 9e année doivent suivre ces étapes :

1. Comprendre les bases

Algèbre : Nécessité de maîtriser les connaissances de base du programme de 9e année, notamment :

Équations du premier et du deuxième degré, solutions et propriétés.

Formules relatives à la géométrie plane et solide, en particulier les théorèmes relatifs aux triangles, aux cercles et aux formes géométriques de base.

Résoudre des problèmes en établissant des équations

Géométrie : Connaissances, théorèmes sur les cercles, les quadrilatères inscrits et leurs propriétés, démonstration des triangles semblables et application des propriétés des triangles semblables,...

Statistiques et probabilités : vous devez être familiarisé avec les concepts statistiques de base tels que les graphiques de fréquence, les tableaux de fréquence et les calculs de probabilité simples, car ce sont des sections qui peuvent apparaître à l'examen.

2. Entraînez-vous à résoudre de vrais problèmes mathématiques

Mathématiques appliquées : Les élèves doivent s'entraîner à résoudre des problèmes liés à la vie réelle, à résoudre des problèmes en établissant des équations, des systèmes d'équations, des problèmes de production et de gestion ou des problèmes liés à la géométrie spatiale.

Appliquer les connaissances à la pratique : Pratiquez des problèmes liés à la mesure et au calcul du volume et de la surface dans des situations pratiques. Cela aide les étudiants à mieux comprendre comment les mathématiques sont appliquées dans la vie.

3. Pratiquez la pensée logique et les compétences analytiques

Preuve mathématique : Améliorer la pratique des problèmes de preuve géométriques et algébriques. En particulier, les problèmes nécessitant la démonstration de relations entre des éléments dans un plan ou une géométrie spatiale sont essentiels pour améliorer la pensée logique.

Analyser et résoudre les problèmes : Entraînez-vous à analyser le problème, en comprenant clairement les exigences de chaque question avant de commencer à le résoudre. Cela permet d’éviter toute confusion et d’augmenter la précision pendant le test.

Source : https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm