Vorgeschlagene Mathe-Antworten für die Aufnahmeprüfung der 10. Klasse in Hanoi im Jahr 2025

Das Hanoi Department of Education and Training hat Beispielfragen für 7 Fächer für die Aufnahmeprüfung der 10. Klasse im Jahr 2025 bekannt gegeben. Diese 7 Fächer umfassen Literatur, Mathematik, Fremdsprachen, Naturwissenschaften, Geschichte und Geographie, Staatsbürgerkunde und Informationstechnologie.

Beispielhafte Mathematikprüfung für die Aufnahmeprüfung der 10. Klasse im Jahr 2025 in Hanoi (Screenshot).

Im Fach Mathematik besteht das Prüfungswissen aus 3 Teilen: Zahlen und Algebra zählen 4,5 Punkte, Geometrie und Messung zählen 4 Punkte, Statistik und Wahrscheinlichkeit zählen 1,5 Punkte.

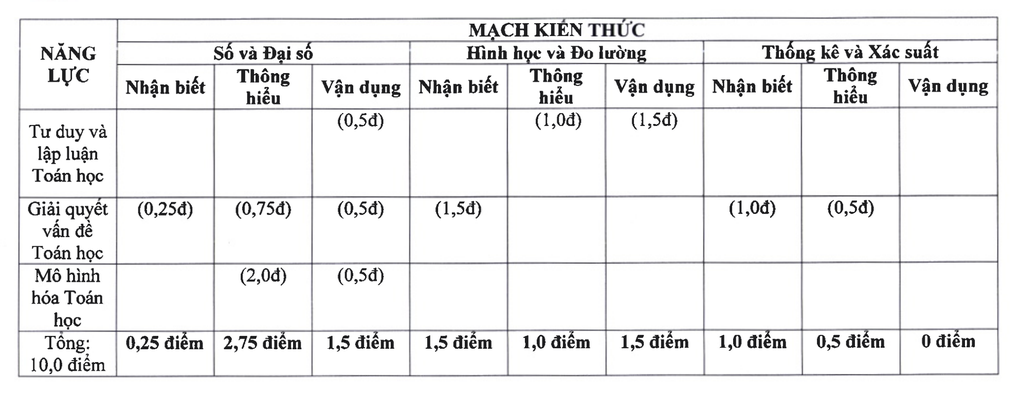
Mathe-Wissenszirkel für die Aufnahmeprüfung der 10. Klasse in Hanoi im Jahr 2025 (Screenshot).

>> Detaillierte Lösungsvorschläge für die Mathematikprüfung für die 10. Klasse in Hanoi im Jahr 2025 von Lehrern der Fachabteilung von tuyensinh247 finden Sie HIER

Überprüfung des Mathe-Illustrationstests

Laut Lehrer Do Van Bao ist die allgemeine Struktur der Prüfung wie folgt aufgebaut:

Teil I: (1,5 Punkte) Enthält 2 Fragen zu Statistik und Wahrscheinlichkeit.

- Datenstatistiken, Diagramme

- Wahrscheinlichkeit

Teil II: (1,5 Punkte) Enthält 3 Fragen zu algebraischen Ausdrücken, ähnlich wie Frage I in den Prüfungen der Vorjahre.

- Berechnen Sie Ausdruckswerte und testen Sie die Grundkenntnisse der Schüler

- Vereinfachen Sie den Ausdruck

- Zusätzliche Fragen zur Differenzierung der Schüler

Teil III: (2,5 Punkte) Enthält 3 Fragen zu Gleichungssystemen und quadratischen Gleichungen.

- Frage 1,2: Lösen Sie reale Probleme, indem Sie ein Gleichungssystem aufstellen, Gleichungen aufstellen

- Frage 3 Quadratische Gleichung

Lektion IV. Geometrie

- Räumliche Geometrie

- Probleme mit Kreisen

Lektion V. Fortgeschrittene Probleme zu geometrischen Extrema im Zusammenhang mit praktischen Faktoren.

Gesamtpunktzahl: 10 Punkte, gleichmäßig verteilt auf die Bereiche Grundlagen- und Aufbauwissen, von Algebra, Geometrie bis hin zu praktischen Anwendungen.

Kommentare zu Wissensinhalten

Algebra-Teil: Beinhaltet grundlegende Inhalte wie Berechnungen mit Ausdrücken, quadratische Gleichungen und Anwendungen. Das Neue am Illustrationstest ist, dass er viele Fragen enthält, die sich mit Problemen aus dem wirklichen Leben befassen und den Schülern helfen, sich Problemen des Lebens mithilfe der Mathematik zu nähern.

Abschnitt Geometrie: Beinhaltet bekannte Inhalte wie ebene Geometrie, Probleme im Zusammenhang mit Kreisen und einbeschriebenen Vierecken, räumliche Geometrie, geometrische Beweise und geometrische Anwendungen in der Praxis. Die Prüfung erfordert von den Studierenden ein gutes räumliches Vorstellungsvermögen und die Fähigkeit, geometrische Theorien auf praktische Probleme anzuwenden.

Abschnitt „Statistik und Wahrscheinlichkeit“: ist im Vergleich zu den Prüfungen des Vorjahres neuer Inhalt, erscheint in Lektion I und erfordert von den Schülern die Analyse von Diagrammen und die Berechnung von Wahrscheinlichkeiten. Dieser Inhalt hat praktische Anwendung und erscheint häufig in neuen Lehrbuchprogrammen.

Anmerkungen zum Schwierigkeitsgrad

Grund- und Mittelstufe: Fragen zum Auswerten von Ausdrücken, Lösen quadratischer Gleichungen und Berechnen von Wahrscheinlichkeiten liegen alle auf Grund- und Mittelstufe. Um diese Fragen beantworten zu können, müssen die Studierenden nur über Grundkenntnisse verfügen.

Oberstufe: Fragen zu geometrischen Beweisen, praktische Probleme der Raumgeometrie sowie Probleme der Bankzinsberechnung erfordern ein gutes logisches Denkvermögen und die Fähigkeit zur praktischen Anwendung der Kenntnisse. Diese Fragen stellen für durchschnittliche Schüler oft eine Herausforderung dar.

Die Musterprüfung von Hanoi orientiert sich eng am neuen Programm der allgemeinen Bildung und legt den Schwerpunkt auf eine umfassende Prüfung der Kenntnisse und Fähigkeiten der Schüler, insbesondere ihrer Fähigkeit, diese in der Praxis anzuwenden.

Die Prüfung behält 60–70 % ihrer traditionellen Struktur bei, wurde jedoch hinsichtlich Inhalt und Fragenstellung erneuert, sodass eine umfassendere Beurteilung der Studierenden möglich ist.

Der Schwierigkeitsgrad der Prüfung ist moderat, mit deutlicher Differenzierung zur Auswahl guter Studierender.

In den vergangenen Jahren kam es in der Prüfung oft zu einer deutlichen Unterscheidung zwischen guten und durchschnittlichen Schülern durch reine Algebra- und Geometriefragen. Der simulierte Test hat ein praktisches Element hinzugefügt, das von den Schülern nicht nur Wissen verlangt, sondern auch, dass sie verstehen, wie sie dieses Wissen auf bestimmte Situationen anwenden können.

Die Struktur der Anschauungsprüfung wurde in diesem Jahr im Vergleich zu den Vorjahren deutlich erneuert, mit einer Klassifizierung der Wissensinhalte in den Lektionen, einer Verflechtung der Fragetypen und insbesondere einer Zunahme praktischer Probleme. Dies spiegelt die Ausrichtung des neuen Bildungsprogramms wider, das sich stärker darauf konzentriert, die Fähigkeit der Schüler zu testen, Wissen anzuwenden und Denken zu synthetisieren.

Um die Prüfung gut zu bestehen, benötigen Schüler der 9. Klasse:

Um sich optimal auf die Aufnahmeprüfung der 10. Klasse mit dem gleichen Aufbau und Inhalt wie die Musterprüfung vorzubereiten, müssen Schüler der 9. Klasse folgende Schritte befolgen:

1. Beherrschen Sie die Grundlagen

Algebra: Im Programm der 9. Klasse müssen grundlegende Kenntnisse erworben werden, darunter:

Gleichungen ersten und zweiten Grades, Lösungen und Eigenschaften.

Formeln im Zusammenhang mit ebener und räumlicher Geometrie, insbesondere Theoreme im Zusammenhang mit Dreiecken, Kreisen und grundlegenden geometrischen Formen.

Lösen Sie Probleme durch Aufstellen von Gleichungen

Geometrie: Kenntnisse, Theoreme über Kreise, einbeschriebene Vierecke und Eigenschaften, Beweis ähnlicher Dreiecke und Anwendung von Eigenschaften ähnlicher Dreiecke, …

Statistik und Wahrscheinlichkeit: Sie müssen mit grundlegenden statistischen Konzepten wie Häufigkeitsdiagrammen, Häufigkeitstabellen und einfachen Wahrscheinlichkeitsberechnungen vertraut sein, da diese Abschnitte in der Prüfung vorkommen können.

2. Üben Sie das Lösen echter mathematischer Probleme

Angewandte Mathematik: Die Studierenden müssen mit Problemen aus dem wirklichen Leben, Problemlösungen durch Aufstellen von Gleichungen, Gleichungssystemen, Produktions- und Managementproblemen oder Problemen der räumlichen Geometrie üben.

Wissen in der Praxis anwenden: Üben Sie Aufgaben rund um das Messen und Berechnen von Volumen und Fläche in praktischen Situationen. Dies hilft den Schülern, besser zu verstehen, wie Mathematik im wirklichen Leben angewendet wird.

3. Üben Sie logisches Denken und analytische Fähigkeiten

Mathematischer Beweis: Verbessern Sie die Praxis geometrischer und algebraischer Beweisprobleme. Insbesondere Probleme, bei denen die Beziehungen zwischen Elementen in einer ebenen oder räumlichen Geometrie aufgezeigt werden müssen, sind für die Verbesserung des logischen Denkens von wesentlicher Bedeutung.

Probleme analysieren und lösen: Üben Sie die Analyse des Problems und machen Sie sich die Anforderungen jeder Frage klar, bevor Sie mit der Lösung beginnen. Dies hilft, Verwirrung zu vermeiden und die Genauigkeit während des Tests zu erhöhen.

Quelle: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm