علماء يجدون حلاً لمشكلة هندسية كلاسيكية استمرت لأكثر من قرن

رسم توضيحي لمسألة هندسية.

وبحسب صحيفة ساوث تشاينا مورنينج بوست، نجح عالم الرياضيات هونغ وانغ -الذي يعمل حاليا أستاذا مشاركا في معهد كورانت للعلوم الرياضية بجامعة نيويورك (الولايات المتحدة)- وزميله جوشوا زاهل (من جامعة كولومبيا البريطانية، كندا) للتو في حل واحدة من أصعب مسائل الهندسة في القرنين العشرين والحادي والعشرين: تخمين كاكيا في الفضاء ثلاثي الأبعاد.

ولد هونغ وانغ في مدينة غويلين (الصين)، ودرس في جامعة بكين قبل أن يقوم بالتدريس والبحث في الولايات المتحدة.

نشأت المشكلة عام ١٩١٧، عندما طرح عالم الرياضيات الياباني سويتشي كاكيا السؤال التالي: "ما أصغر مساحة مطلوبة لتدوير إبرة ١٨٠ درجة؟" تُسمى هذه المساحة الدنيا "مجموعة كاكيا".

في الفضاء ثنائي الأبعاد، من السهل تصور تدوير الإبرة لتشكيل دائرة، ولكن إذا كان الدوران أكثر مرونة، مثل تحريك الإبرة أثناء الدوران، يمكن أن تكون المنطقة التي تمسحها الإبرة أصغر.

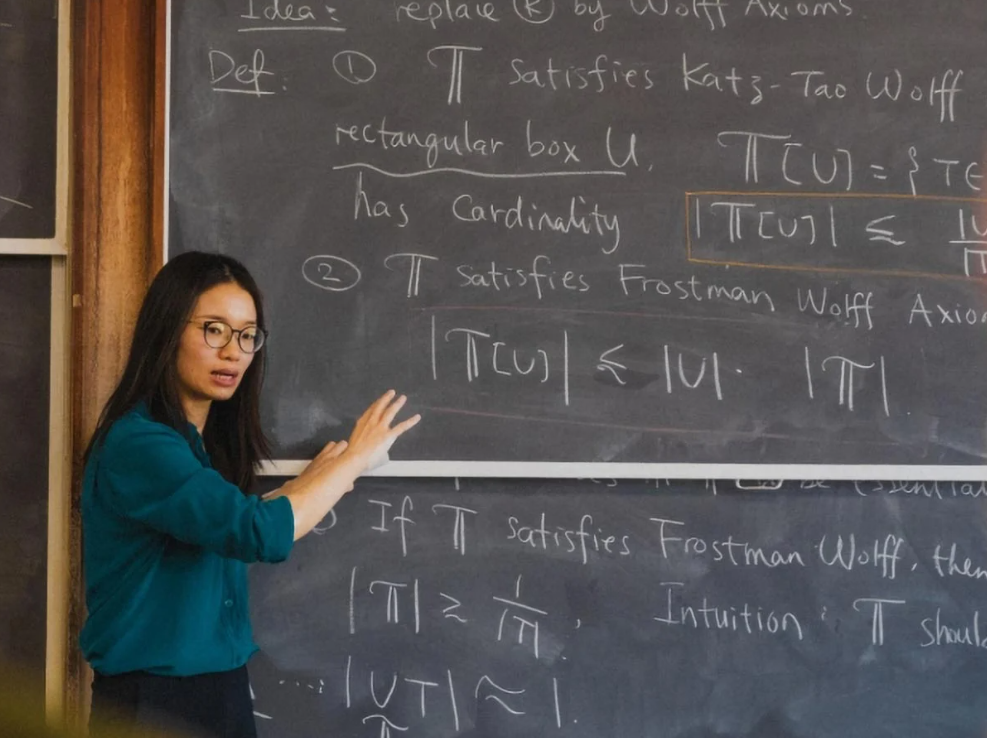
علماء يجدون حلاً لمشكلة هندسية استمرت لأكثر من قرن من الزمان.

عندما يتم إدخال المشكلة إلى ثلاثة أبعاد، تصبح المشكلة أكثر تعقيدًا. يقول تخمين كاكيا أنه إذا كنت تريد تدوير الإبرة في جميع الاتجاهات، فيجب أن تكون المساحة المطلوبة كبيرة بما يكفي في جميع الأبعاد الثلاثة - ولا يمكن ضغطها في مكان صغير جدًا أو رقيق جدًا.

في ورقة بحثية نُشرت مؤخرًا على منصة arXiv، أظهر وانج وزال أنه في الفضاء ثلاثي الأبعاد، لا تحتاج المنطقة اللازمة لتدوير الإبرة إلى أن يكون لها شكل واضح، ولكن يجب أن تظل كبيرة بما يكفي في جميع الأبعاد الثلاثة. وبفضل ذلك، تمكنوا من حل هذه المشكلة - وهذا يعتبر اكتشافًا مهمًا للغاية في الرياضيات اليوم.

ووصف البروفيسور تيرينس تاو - أحد أبرز علماء الرياضيات في العالم - هذا الأمر بأنه "تقدم مذهل". وقال الخبراء أيضًا إن هذا العمل لا يوسع فهم الهندسة فحسب، بل يمكن أن يؤثر أيضًا على العديد من المجالات مثل معالجة الصور، والاتصالات اللاسلكية، وعلوم الكمبيوتر، والتشفير - حيث يعد فهم الحركات والتفاعلات في الفضاء مهمًا للغاية.

"لا أبالغ، ولكن هذا حل نادر انتظرنا ظهوره مئات السنين"، هذا ما قاله أستاذ الرياضيات نتس كاتز، الذي يدرس في جامعة رايس (الولايات المتحدة).

وبحسب البروفيسور جوث لاري، المحاضر في معهد ماساتشوستس للتكنولوجيا (الولايات المتحدة)، فإن فرضية كاكيا هي الأساس لـ"برج" من الفرضيات الأكبر في مجال الهندسة. إن حل هذه الفرضية سيعطي المستويات العليا من برج المعرفة فرصة للوصول إليها والتغلب عليها.

كنت أظن أن هذه مسألة هندسية بسيطة وأساسية، لكنها في الواقع معقدة للغاية. سعى العديد من كبار علماء الرياضيات إلى حل هذه المسألة، لكن معظمهم لم يحقق سوى نتائج محدودة، ولم تكن منهجية، ولا يمكن اعتبارها حلاً كاملاً، كما أشار البروفيسور غوث لاري.

فونج آنه (المصدر: Science Daily، SCMP)

المصدر: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-geometry-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html